Partial Identifiability
for NMF
Samyar Modabber
TU Chemnitz
2023/02/08
Content
Introduction
Exact NMF
Full Identifability
Partial Identifability
Part 1:
Introduction
LDR (Linear dimensionality reduction)
Find small number $r$ of basis vectors such that
each data point is well approximated by a linear combination of
these basis vectors.
- Input: $\left\{ {{x}_{j}}\in {{\mathbb{R}}^{m}} \right\}_{j=1}^{n}$
- Output: $\left\{ {{w}_{k}}\in {{\mathbb{R}}^{m}} \right\}_{k=1}^{r}$
- Goal: Min $r$ such that ${{x}_{j}}\approx \sum\limits_{k=1}^{r}{{{w}_{k}}{{h}_{kj}}}$
Geometrical interpretation of LDR
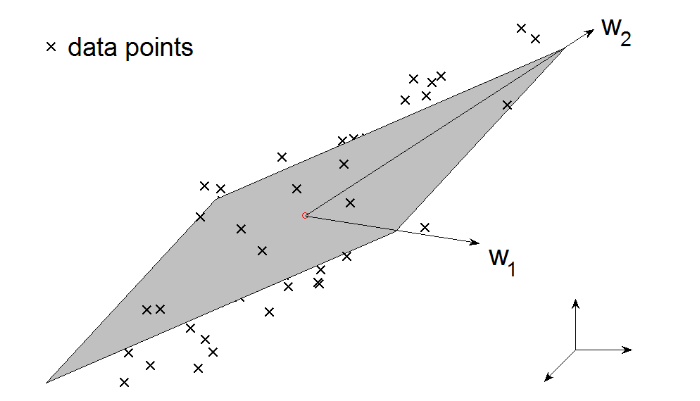 N. Gillis, "Nonnegative Matrix Factorization", SIAM, Philadelphia, 2020.
N. Gillis, "Nonnegative Matrix Factorization", SIAM, Philadelphia, 2020.
LRMA (low-rank matrix approximation)
- Input: $X\in{{\mathbb{R}}^{m\times n}}$
- Output: $W\in {{\mathbb{R}}^{m\times r}}, H \in {{\mathbb{R}}^{r\times n}}$
- Goal: MIN $r$ such that $X\approx WH$
LDR is equivalent to LRMA
\[\begin{matrix} {} & LDR & \Leftrightarrow & LRMA \\ \forall j\in {{\mathbb{N}}_{n}} & {{x}_{j}} & {} & X\left( :,j \right) \\ \forall k\in {{\mathbb{N}}_{r}} & {{w}_{k}} & {} & W\left( :,k \right) \\ \forall j\in {{\mathbb{N}}_{n}} & {{h}_{j}} & {} & H\left( :,j \right) \\ \end{matrix}\]
NMF (Nonnegative matrix factorization)
-
Input:
nonnegetive matrix: $X\in \mathbb{R}_{+}^{m\times n}$ ,
factorization rank: $r$,
distance measure: $D:\ \mathbb{R}_{+}^{m\times n}\times \mathbb{R}_{+}^{m\times n}\to {{\mathbb{R}}_{+}}$ - Output: $W\in \mathbb{R}_{+}^{m\times r},\ H\in \mathbb{R}_{+}^{r\times n}$
- Goal: $$\underset{W,H}{\mathop{\min }}\,D\left( X,WH \right)$$
Basic Definitions
Let $A\in \mathbb{R}_{{}}^{m\times n}\ $ and ${{e}^{T}}=\left[ 1\ \cdots 1 \right]$, then we define:
- 1) Column space: $col\left( A \right):=\left\{ \left. Ay \right|y\in {{\mathbb{R}}^{n}} \right\}$
- 2) Affin hull: $aff\left( A \right):=\left\{ \left. Ay \right|y\in {{\mathbb{R}}^{n}},\ {{e}^{T}}y=1 \right\}$
- 3) Conical hull: $cone\left( A \right):=\left\{ \left. Ay \right|y\in {{\mathbb{R}}^{n}},\ y\ge 0 \right\}$
- 4) Convex hull: $conv\left( A \right):=\left\{ \left. Ay \right|y\in {{\mathbb{R}}^{n}},\ {{e}^{T}}y=1,\ y\ge 0 \right\}$
-
5) Support: $\operatorname{supp}\left( A \right)=\left\{ \left.
\left( i,j \right) \right|A\left( i,j \right)\ne 0 \right\}$,
for vectors $\operatorname{supp}\left( a \right)=\left\{ \left. j \right|{{a}_{j}}\ne 0 \right\}$ - 6) A is stochastic if ${{e}^{T}}A={{e}^{T}}$
- 7) Normalized of A: $\theta \left( A \right):=\left[ \begin{matrix}{}^{{{a}_{1}}}/{}_{{{\left\| {{a}_{1}} \right\|}_{1}}} & \cdots & {}^{{{a}_{n}}}/{}_{{{\left\| {{a}_{n}} \right\|}_{1}}} \\ \end{matrix} \right]$
- 8) Nonnegative Orthant: $\mathbb{R}_{+}^{n}:=\left\{ \left. y \right|y\in {{\mathbb{R}}^{n}},\ y\ge 0 \right\}$
- 9) Probability Simplex: $\Delta ={{\Delta }^{n}}:=\left\{ \left. y \right|y\in {{\mathbb{R}}^{n}},\ {{e}^{T}}y=1,\ y\ge 0 \right\}=conv\left( I \right)$
Part 2:
Exact NMF
Exact NMF
Decomposition $R=C{{S}^{T}}$ of $R\in \mathbb{R}_{+}^{m\times n}$ is called
an Exact NMF of size $r$ and we write $R\ \overset{Exact}{\mathop{=}}\,C{{S}^{T}}$ if:
$C\in \mathbb{R}_{+}^{m\times r},\ S\in \mathbb{R}_{+}^{n\times r}$
Fact
For an Exact NMF $R\overset{Exact}{\mathop{=}}\,C{{S}^{T}}$,
w.l.o.g.
we can assume $R,\ C\ and \ {{S}^{T}}$ are stochastic .
Proof: First remove zero columns then define
$$\begin{align*} {{R}_{n}}\left( :,j \right) &:=\frac{R\left( :,j \right)}{{{e}^{T}}R\left( :,j \right)}=\frac{\sum\limits_{k=1}^{r}{C\left( :,k \right)S\left( j,k \right)}}{{{e}^{T}}R\left( :,j \right)} \\ & =\sum\limits_{k=1}^{r}{\left( \frac{C\left( :,k \right)}{{{e}^{T}}C\left( :,j \right)} \right)\left( \frac{{{e}^{T}}C\left( :,j \right)}{{{e}^{T}}R\left( :,j \right)}S\left( j,k \right) \right)} \\ & =\sum\limits_{k=1}^{r}{{{C}_{n}}\left( :,k \right){{S}_{n}}\left( j,k \right)} \\ \end{align*}$$
Hence ${{R}_{n}}$and ${{C}_{n}}$are stochastic and for $S_{n}^{T}$: ${{e}^{T}}S_{n}^{T}=\left( {{e}^{T}}{{C}_{n}} \right)S_{n}^{T}={{e}^{T}}{{R}_{n}}={{e}^{T}}$
NPP (Nested Polytope Problem)
A NPP with parameter $d$ and $p$Input: ${{P}_{inn}},\ {{P}_{out}}$ such that:
1) full-dimensional inner polytope: ${{P}_{inn}}:=\ conv\left( \left[ {{v}_{1}},{{v}_{2}},\cdots ,{{v}_{n}} \right] \right)\subseteq {{\mathbb{R}}^{d}}$
2) full-dimensional outer polytope: ${{P}_{out}}:=\ \left\{ \left. x\in {{\mathbb{R}}^{d}} \right|Fx+g\ge 0 \right\}$
where $F\in \mathbb{R}_{{}}^{m\times r},\ g\in {{\mathbb{R}}^{m}}$
Output: ${{P}_{bet}}$ with $p$ vertices such that $p\ge d+1$
Goal: ${{P}_{inn}}\subseteq {{P}_{bet}}\subseteq {{P}_{out}}$
Theorem 1
An Exact NMF problem with $r\text{ }=\text{ }rank\left( R \right)$
$$\Leftrightarrow $$ $$\Leftrightarrow $$ $$\Leftrightarrow $$
An NPP with $d\text{ }=\text{ }rank\left( R \right)\text{ }-\text{ }1$
and $p\text{ }=\text{ }d\text{ }+\text{ }1$.
Example 1
${{P}_{inn}}:=\ conv\left( \left[ {{v}_{1}}=>\left[ \begin{matrix} 0.5 \\ 0 \\ \end{matrix} \right],{{v}_{2}}=\left[ \begin{matrix} 0 \\ 0.5 \\ \end{matrix} \right],{{v}_{3}}=\left[ \begin{matrix} 0.25 \\ 0.75 \\ \end{matrix} \right],{{v}_{4}}=\left[ \begin{matrix} 0.75 \\ 0.25 \\ \end{matrix} \right] \right] \right)\subseteq {{\mathbb{R}}^{2}}$
${{P}_{out}}:=\ \left\{ \left. x\in {{\mathbb{R}}^{2}} \right|Fx+g={{\left[ \begin{matrix} 0 & 0 & 1 & -1 \\ 1 & -1 & 0 & 0 \\ \end{matrix} \right]}^{T}}x+{{\left[ \begin{matrix} 0 & 1 & 0 & 1 \\ \end{matrix} \right]}^{T}}\ge 0 \right\}$
$R\left( :,j \right)=F{{v}_{j}}+g=\frac{1}{4}\left[ \begin{matrix} 0 & 2 & 3 & 1 \\ 4 & 2 & 1 & 3 \\ 2 & 0 & 1 & 3 \\ 2 & 4 & 3 & 1 \\ \end{matrix} \right]$
${{P}_{bet}}:=\ conv\left( \left[ {{s}_{1}}=\left[ \begin{matrix} 0 \\ 0 \\ \end{matrix} \right],{{s}_{2}}=\left[ \begin{matrix} 0 \\ 1 \\ \end{matrix} \right],{{s}_{3}}=\left[ \begin{matrix} 1 \\ 0 \\ \end{matrix} \right] \right] \right)$
$C\left( :,j \right)=F{{s}_{j}}+g=\left[ \begin{matrix} 0 & 0 & 1 \\ 1 & 1 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \\ \end{matrix} \right]$
Illustration of the NPP (Example 1)
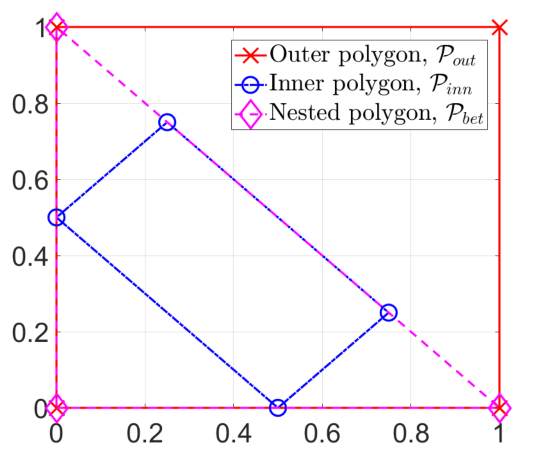 N. Gillis and R. Rajkó, "Partial Identifiability for Nonnegative Matrix Factorization", SIAM J. on Matrix Analysis and Applications 44 (1), pp. 27-52, 2023.
N. Gillis and R. Rajkó, "Partial Identifiability for Nonnegative Matrix Factorization", SIAM J. on Matrix Analysis and Applications 44 (1), pp. 27-52, 2023.
Part 3:
Full
identifiability
Full identifiability
Exact NMF $R\ \overset{Exact}{\mathop{=}}\,{{C}_{*}}S_{*}^{T}$ of $R\in \mathbb{R}_{+}^{m\times n}$ is called
a (full) identifiability of rank $r$
and we write $R\ \overset{Full}{\mathop{=}}\,C{{S}^{T}}$ if:
$$\forall \ R \: \overset{Exact}{\mathop{=}}\: C{{S}^{T}}\ \exists \: \pi :{{\mathbb{N}}_{r}}\to {{\mathbb{N}}_{r}}\ \exists \: 0 < \alpha \in {{\mathbb{R}}^{r}}$$ $$C\left( :,k \right)={{\alpha }_{k}}{{C}_{*}}\left( :,{{\pi }_{k}} \right)\ ,\ \ S\left( :,k \right)^{T}=\frac{1}{{{\alpha }_{k}}}{{S}_{*}}\left( :,{{\pi }_{k}} \right)^{T}$$
Full identifiability also known as unique, or essentially unique.Remark
Full identifiability with Matrix notation
$\forall \ R\overset{Exact}{\mathop{=}}\,C{{S}^{T}}$, there exists
a permutation matrix $\Pi \in {{\left\{ 0,1 \right\}}^{r\times r}}$ and
a nonsingular diagonal scaling matrix $D$
such that \[C={{C}_{*}}\Pi D\ \wedge \ {{S}^{T}}={{D}^{-1}}{{\Pi }^{T}}S_{*}^{T}\]
Theorem 2
$$R\ \overset{Full}{\mathop{=}}\,{{C}_{*}}S_{*}^{T}\ \Rightarrow \ \ $$ $ \forall j,{j}'\ \ j\ne {j}'\ \ \ \operatorname{supp}\left( {{C}_{*}}\left( :,j \right) \right)\not\subset \operatorname{supp}\left( {{C}_{*}}\left( :,{j}' \right) \right)$
Separability
$C\in \mathbb{R}_{{}}^{m\times r}$ with $m\text{ }\ge \text{ }r$ is called separable if
There exists an index set $K$ of size $r$ such that $C\left( K,: \right)\in \mathbb{R}_{{}}^{r\times r}$ is a nonsingular diagonal matrix.
Theorem 3
The Exact NMF $R\overset{Exact}{\mathop{=}}\,{{C}_{*}}S_{*}^{T}$
is a Full Identifiability
if ${{C}_{*}}$ and $S_{*}^{T}$ are separable.
SSC (sufficiently scattered condition)
$C\in \mathbb{R}_{{}}^{m\times r}$ with $m \ge r$ satisfies $SSC$ if:
1) $L:=\left\{ \left. x\in \mathbb{R}_{+}^{r} \right|{{e}^{T}}x\ge \sqrt{r-1}{{\left\| x \right\|}_{2}} \right\}\subseteq cone\left( {{C}^{T}} \right)$
$L$ is a Lorentz cone, also known as a second-order cone or an ice cream cone.
2) Does not exist any orthogonal matrix $Q$ ($Q{{Q}^{T}}=I\ $) such that $$cone\left( {{C}^{T}} \right)\subseteq cone\left( Q \right),$$ except for permutation matrices.
Theorem 4
The Exact NMF $R\overset{Exact}{\mathop{=}}\,{{C}_{*}}S_{*}^{T}$
is a Full Identifiability
if ${{C}_{*}}$ and $S_{*}^{T}$ satisfy the SSC.
Separability vs. SSC
 N. Gillis, "Nonnegative Matrix Factorization", SIAM, Philadelphia, 2020.
N. Gillis, "Nonnegative Matrix Factorization", SIAM, Philadelphia, 2020.
Part 4:
Partial
Identifiability
Partial identifiability
Let $R\ \overset{Exact}{\mathop{=}}\,{{C}_{*}}S_{*}^{T}$. ${{C}_{*}}\left( :,k \right)$ is called identifiable if
$\forall \ R\overset{Exact}{\mathop{=}}\,C{{S}^{T}}\ \exists j\ \ \exists \alpha >0\ \ \ \ {{C}_{*}}\left( :,k \right)=\alpha C\left( :,j \right)$
Theorem 5
If $R\ \overset{\ Exact}{\mathop{=}}\,{{C}_{*}}S_{*}^{T}$ and ${{C}_{*}}\left( :,k \right)$is identifiable,
then
$$\ \forall j\ \ j\ne k\ \ \operatorname{supp}\left( {{C}_{*}}\left( :,j \right) \right)\not\subset \operatorname{supp}\left( {{C}_{*}}\left( :,k \right) \right)$$ $ \left( resp.\ {{S}_{*}} \right)$
Theorem 6
Restricted DBU (Data-Based uniqueness)
Let $R\ \overset{Exact}{\mathop{=}}\,{{C}_{*}}S_{*}^{T}$ of size $r$.
Then ${{C}_{*}}\left( :,k \right)$ is identifiable if:
1) FRZRW (Full-rank zero-region window):
$$rank\left( {{C}_{*}}\left( I,: \right) \right)=r-1$$
where $I=\left\{ \left. i \right|{{C}_{*}}\left( i,k \right)=0 \right\}=\text{supp}{{\left( C\left( :,k \right) \right)}^{c}}$
2) SW (Selective window):
$$\exists j\ \exists \alpha >0\ \ \ \ {{S}_{*}}\left( j,: \right)=\alpha e_{\left( k \right)}^{T}$$
Example 2
$R\ \overset{Exact}{\mathop{=}}\,{{C}_{*}}S_{*}^{T}=\left[ \begin{matrix} 2 & 2 & 2 \\ 1 & 3 & 1 \\ 1 & 1 & 3 \\ 0 & 2 & 2 \\ 0 & 1 & 2 \\ \end{matrix} \right]\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right]$
FRZRW:
$I=\left\{ 4,5 \right\}\ \Rightarrow C\left( I,: \right)=\left[ \begin{matrix}
0 & 2 & 2 \\
0 & 1 & 2 \\
\end{matrix} \right]\ \\ \Rightarrow rank\left( C\left( I,: \right) \right)=2=3-1=r-1$
SW:
$\exists j=1\ \exists \alpha =1>0\ \ \ \ {{S}_{*}}\left( 1,: \right)=e_{\left( 1 \right)}^{T}$
Minimal face
Let $C\in \mathbb{R}_{+}^{m\times r}$ be a stochastic matrix and
$y\in \Gamma =col\left( C \right)\bigcap \Delta $.
We define minimal face of $C$ containing $y$ by
$$ \begin{equation*} \begin{aligned} {{F}_{C}}\left( y \right) & =\left\{ \left. x\in \Gamma \right|\text{supp}\left( x \right)\subseteq \text{supp}\left( y \right) \right\} \\ & =\left\{ \left. Cz \right|\text{z}\in {{\mathbb{R}}^{r}}\text{,}\ \ {{\text{e}}^{T}}\text{z=1}\text{,}\ {{y}_{i}}=0\Rightarrow {{\left( Cz \right)}_{i}}=0 \right\} \end{aligned} \end{equation*} $$
All the points in ${{F}_{C}}\left( y \right)$ have to belong to the same facets of $C$ as $y$.
Note
-
A face of a polytope is obtained by intersecting a subset of its facets.
Hence ${{F}_{C}}\left( y \right)$ is the face of $C$ of minimal dimension containing $y$. -
A vertex of a poltyope is a 0-dimensional face, and hence
$y$ is a vertex of $C$ $\Leftrightarrow {{F}_{C}}\left( y \right)=\left\{ y \right\}$.
Lemma 1
Let $C\in \mathbb{R}_{+}^{m\times r}$ be a nonsingular stochastic matrix.
${{C}_{*}}\left( :,k \right)$ has FRZRW condition
$\Leftrightarrow $
$${{F}_{C}}\left( C\left( :,k \right) \right)=\left\{ C\left( :,k \right) \right\}$$
Theorem 7
Let $R\ \overset{Exact}{\mathop{=}}\,{{C}_{*}}S_{*}^{T}$ with $r=rank\left( R \right)$,
${{C}_{*}}\in \mathbb{R}_{+}^{m\times r}$ and $S_{*}^{T}\in \mathbb{R}_{+}^{n\times r}$ are stochastic.
1) it satisfies the selective window condition
2) there exists index set $J$such that $$rank\left( R\left( :,J \right) \right)=r-1\ \\ \\ \ \forall j\in J\ {{F}_{{{C}_{*}}}}\left( {{C}_{*}}\left( :,k \right) \right)\bigcap {{F}_{{{C}_{*}}}}\left( R\left( :,j \right) \right)=\varnothing $$
Example 3
${{P}_{inn}}:=\ conv\left( \left[ {{v}_{1}}=\left[ \begin{matrix} 0.5 \\ 0 \\ \end{matrix} \right],{{v}_{2}}=\left[ \begin{matrix} 0.2 \\ 1 \\ \end{matrix} \right],{{v}_{3}}=\left[ \begin{matrix} 0.8 \\ 1 \\ \end{matrix} \right] \right] \right)\subseteq {{\mathbb{R}}^{2}}$
${{P}_{out}}:=\ \left\{ \left. x\in {{\mathbb{R}}^{2}} \right|Fx+g={{\left[ \begin{matrix} 0 & 0 & 1 & -1 \\ 1 & -1 & 0 & 0 \\ \end{matrix} \right]}^{T}}x+{{\left[ \begin{matrix} 0 & 1 & 0 & 1 \\ \end{matrix} \right]}^{T}}\ge 0 \right\}$
$R=\left[ \begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0.5 & 0.2 & 0.8 \\ 0.5 & 0.8 & 0.2 \\ \end{matrix} \right]=\left[ \begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0.5 & 0 & 1 \\ 0.5 & 1 & 0 \\ \end{matrix} \right]\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 0.8 & 0.2 \\ 0 & 0.2 & 0.8 \\ \end{matrix} \right]={{C}_{*}}S_{*}^{T}$
$C\left( :,1 \right)$ satisfies the selective window and minimal faces of $R\left( :,\left[ 2,3 \right] \right)$do not intersect with minimal faces of $C\left( :,1 \right)$
Illustration of the NPP (Example 3)
 N. Gillis and R. Rajkó, "Partial Identifiability for Nonnegative Matrix Factorization", SIAM J. on Matrix Analysis and Applications 44 (1), pp. 27-52, 2023.
N. Gillis and R. Rajkó, "Partial Identifiability for Nonnegative Matrix Factorization", SIAM J. on Matrix Analysis and Applications 44 (1), pp. 27-52, 2023.
Corollary 1
Let $R\ \overset{Exact}{\mathop{=}}\,{{C}_{*}}S_{*}^{T}$ with $r=rank\left( R \right)$,
${{C}_{*}}\in \mathbb{R}_{+}^{m\times r}$ and $S_{*}^{T}\in \mathbb{R}_{+}^{n\times r}$ are stochastic.
Then $R\ \overset{\ Full}{\mathop{=}}\,{{C}_{*}}S_{*}^{T}$ if
1) $\forall k\ \ {{C}_{*}}\left( :,k \right)$satisfies the selective window.
2) $\forall k,j\ \ \ k\ne j\Rightarrow \ {{F}_{{{C}_{*}}}}\left( {{C}_{*}}\left( :,k \right) \right)\bigcap {{F}_{{{C}_{*}}}}\left( {{C}_{*}}\left( :,j \right) \right)=\varnothing $
Example 4
${{P}_{inn}}:=\ conv\left( \left[ {{v}_{1}}=\left[ \begin{matrix} 0 \\ 0 \\ 0.75 \\ \end{matrix} \right],{{v}_{2}}=\left[ \begin{matrix} 0 \\ 1 \\ 0.25 \\ \end{matrix} \right],{{v}_{3}}=\left[ \begin{matrix} 1 \\ 1 \\ 0.75 \\ \end{matrix} \right] \right] \right)\subseteq {{\mathbb{R}}^{3}}$
${{P}_{out}}:=\ {{\left[ 0,1 \right]}^{3}}$
satisfies the conditions of Theorem 7 for all $k$
since the vertices of ${{P}_{inn}}$ are on (minimal) faces (namely, edges) that do not intersect.
therefore R has a unique exact NMF
Illustration of the NPP (Example 4)
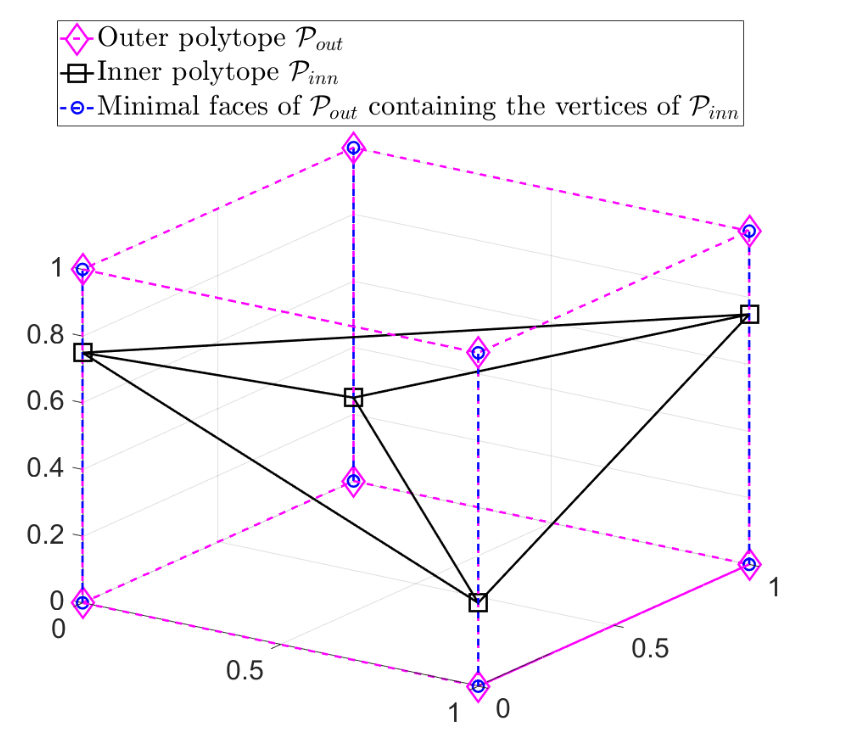 N. Gillis and R. Rajkó, "Partial Identifiability for Nonnegative Matrix Factorization", SIAM J. on Matrix Analysis and Applications 44 (1), pp. 27-52, 2023.
N. Gillis and R. Rajkó, "Partial Identifiability for Nonnegative Matrix Factorization", SIAM J. on Matrix Analysis and Applications 44 (1), pp. 27-52, 2023.
Theorem 8
Let $R\ \overset{Exact}{\mathop{=}} {{C}_{*}}S_{*}^{T}$ with $r=rank\left( R \right)$, ${{C}_{*}}\in \mathbb{R}_{+}^{m\times r}$ and $S_{*}^{T}\in \mathbb{R}_{+}^{n\times r}$
and w.l.o.g $\forall j=1,\ 2,\ ...,\ p;\ {{C}_{*}}\left( :,j \right)$ are identifiable.
Let $J$ be the index set of columns of $R$
that do not contain the support of the first $p$ columns of ${{C}_{*}}$. and
- $rank\left( {{S}_{*}}\left( J,p+1:r \right) \right)=r-p$
-
${{C}_{*}}\left( :,p+1 \right)$ identifiable in
$R\left( :J \right)\overset{Exact}{\mathop{=}}\,{{C}_{*}}\left( :,p+1:r \right){{S}_{*}}{{\left( J,p+1:r \right)}^{T}}$of size $r-p$
then ${{C}_{*}}\left( :,p+1 \right)$ is identifiable in the Exact NMF of $R$ of size $r$.
Lemma 2
Let $R\ \overset{\ Exact}{\mathop{=}}\,{{C}_{*}}S_{*}^{T}$ and $R\ \overset{Exact}{\mathop{=}}\,C{{S}^{T}}$ with size $r=rank\left( R \right)$ and w.l.o.g $C$ and ${{C}_{*}}$ are stochastic. If ${{C}_{*}}\left( :,k \right)$ satisfied following condition:
1) The selective window assumption, i.e., $\exists \alpha >0\ \ \exists j\ \ \ st\ {{C}_{*}}\left( :,k \right)=\alpha R\left( :,j \right)$
2) Is not identifiable in $C$, i.e. $\forall j\ \ \ C\left( :,j \right)\ne {{C}_{*}}\left( :,k \right)$
Then there exists an index set $J$ with $\left| J \right|\ge 2$ such that
$$\forall j\in J\ \ \ \ C\left( :,j \right)\in {{F}_{{{C}_{*}}}}\left( {{C}_{*}}\left( :,k \right) \right)$$
Theorem 9
Let $R\ ={{C}_{*}}S_{*}^{T}$ with size $r=3=rank\left( R \right)$, ${{C}_{*}}\in \mathbb{R}_{+}^{m\times 3}$ and $S_{*}^{T}\in \mathbb{R}_{+}^{n\times 3}$ and w.l.o.g $R$, ${{C}_{*}}$ and $S_{*}^{T}$ are stochastic.
W.l.o.g let ${{C}_{*}}\left( :,1 \right)$ and ${{C}_{*}}\left( :,2 \right)$satisfied selective window and their support do not contain each other.
Then these two columns are identifiable if $\exists R\left( :,j \right)$ such that:
IF ${{F}_{{{C}_{*}}}}\left( {{C}_{*}}\left( :,1 \right) \right)\bigcap {{F}_{{{C}_{*}}}}\left( {{C}_{*}}\left( :,2 \right) \right)=\varnothing $,
\[R\left( :,j \right)\notin \ conv\left( \left[ {{C}_{*}}\left( :,1 \right),{{F}_{{{C}_{*}}}}\left( {{C}_{*}}\left( :,2 \right) \right) \right] \right)\bigcup conv\left( \left[ {{C}_{*}}\left( :,2 \right),{{F}_{{{C}_{*}}}}\left( {{C}_{*}}\left( :,1 \right) \right) \right] \right)\]
Else
\[R\left( :,j \right)\notin \ conv\left( \left[ {{F}_{{{C}_{*}}}}\left( {{C}_{*}}\left( :,1 \right) \right),{{F}_{{{C}_{*}}}}\left( {{C}_{*}}\left( :,2 \right) \right) \right] \right)\]
Algotithm

Refrences
- N. Gillis and R. Rajkó, "Partial Identifiability for Nonnegative Matrix Factorization", SIAM J. on Matrix Analysis and Applications 44 (1), pp. 27-52, 2023.
- N. Gillis, "Nonnegative Matrix Factorization", SIAM, Philadelphia, 2020.

Thank you
Please find the presentation on my GitHub: https://github.com/samyarmodabber/TUC_Seminar_NMF
