Deep Reinforcement Learning
A3C - DDPG - PPO
Professur für Künstliche Intelligenz - Fakultät für Informatik
1 - A3C: Asynchronous advantage actor-critic

Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T. P., Harley, T., et al. (2016). Asynchronous Methods for Deep Reinforcement Learning. ICML. arXiv:1602.01783
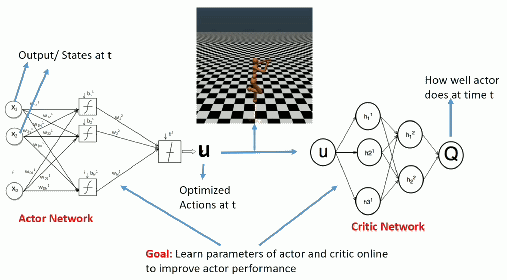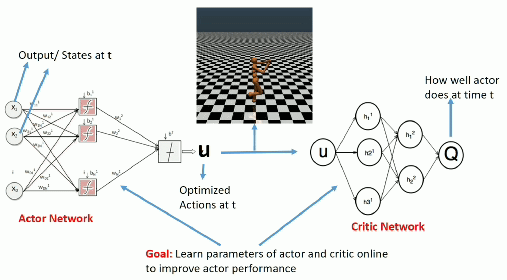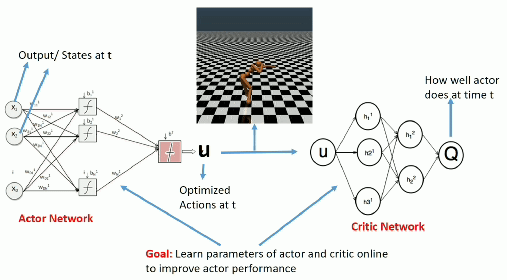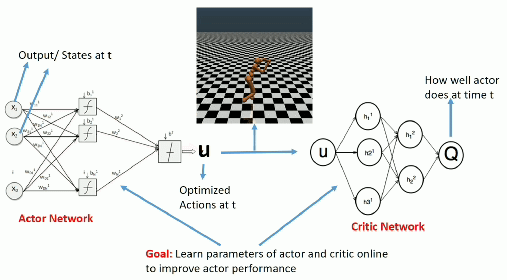
Advantage actor-critic
- Let’s consider an n-step advantage actor-critic architecture where the Q-value of the action (s_t, a_t) is approximated by the n-step return:
Q^{\pi_\theta}(s_t, a_t) \approx R_t^n = \sum_{k=0}^{n-1} \gamma^{k} \, r_{t+k+1} + \gamma^n \, V_\varphi(s_{t+n})
- The actor \pi_\theta(s, a) uses PG with baseline to learn the policy:
\nabla_\theta \mathcal{J}(\theta) = \mathbb{E}_{s_t \sim \rho_\theta, a_t \sim \pi_\theta}[\nabla_\theta \log \pi_\theta (s_t, a_t) \, (R_t^n - V_\varphi(s_t)) ]
- The critic V_\varphi(s) approximates the value of each state:
\mathcal{L}(\varphi) = \mathbb{E}_{s_t \sim \rho_\theta, a_t \sim \pi_\theta}[(R^n_t - V_\varphi(s_t))^2]
Advantage actor-critic
Advantage actor-critic
The advantage actor-critic is strictly on-policy:
The critic must evaluate actions selected the current version of the actor \pi_\theta, not an old version or another policy.
The actor must learn from the current value function V^{\pi_\theta} \approx V_\varphi.
\begin{cases} \nabla_\theta \mathcal{J}(\theta) = \mathbb{E}_{s_t \sim \rho_\theta, a_t \sim \pi_\theta}[\nabla_\theta \log \pi_\theta (s_t, a_t) \, (R^n_t - V_\varphi(s_t)) ] \\ \\ \mathcal{L}(\varphi) = \mathbb{E}_{s_t \sim \rho_\theta, a_t \sim \pi_\theta}[(R^n_t - V_\varphi(s_t))^2] \\ \end{cases}
- We cannot use an experience replay memory to deal with the correlated inputs, as it is only for off-policy methods.
Distributed RL
- We cannot get an uncorrelated batch of transitions by acting sequentially with a single agent.
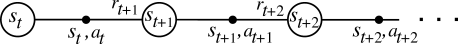
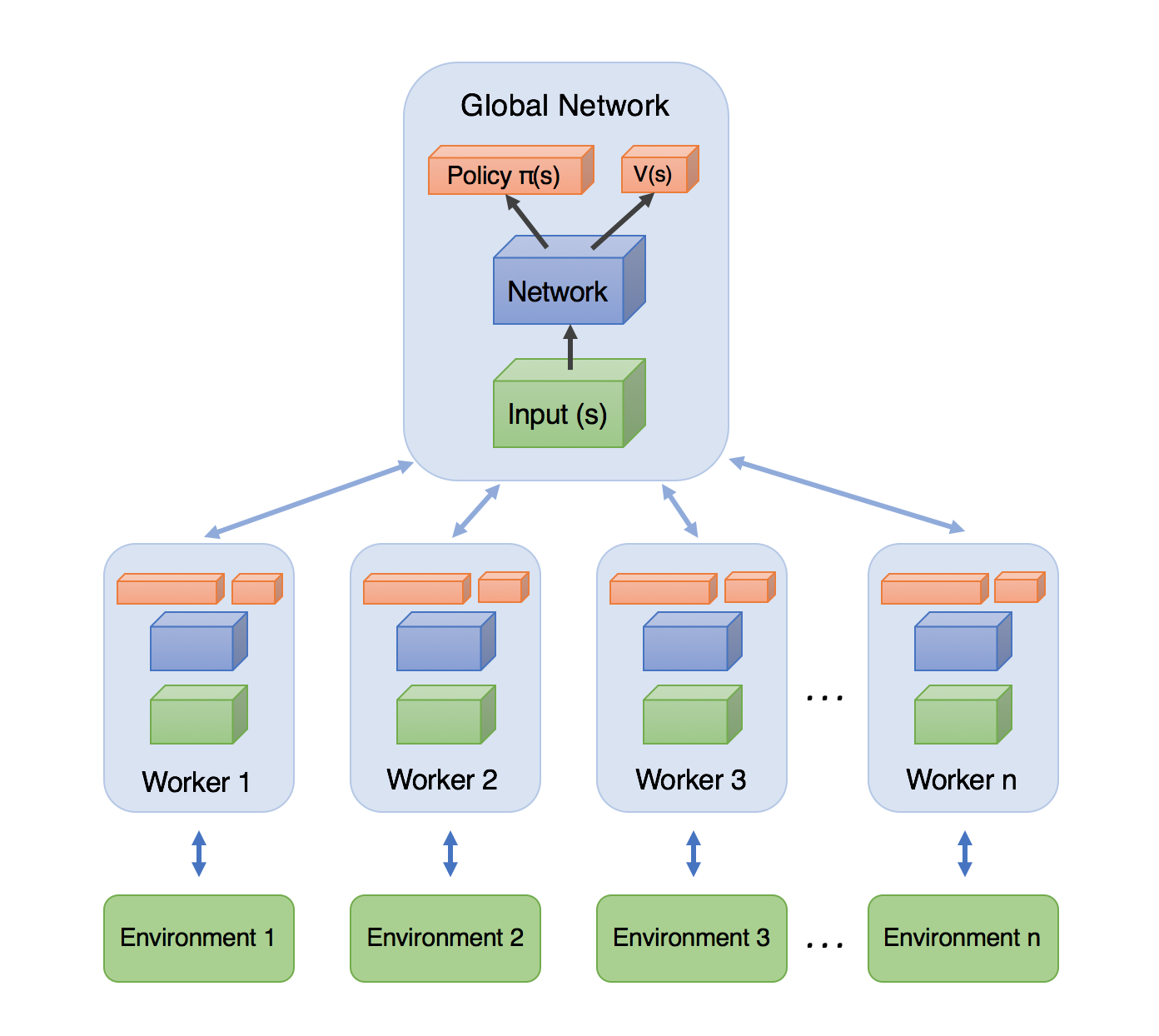
- A simple solution is to have multiple actors with the same weights \theta interacting in parallel with different copies of the environment. See GORILA, APE-X, R2D2.
Each rollout worker (actor) starts an episode in a different state: at any point of time, the workers will be in uncorrelated states.
From time to time, the workers all send their experienced transitions to the learner which updates the policy using a batch of uncorrelated transitions.
After the learner update, the workers use the new policy to collect new transitions.
Distributed RL
Having multiple workers interacting with different environments is easy in simulation (Atari games).
With physical environments, working in real time, it requires lots of money…
A3C: Asynchronous advantage actor-critic
- In A3C, the workers do not simply collect experiences, but also compute gradients on their collected transitions and send them to the global network.
Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T. P., Harley, T., et al. (2016). Asynchronous Methods for Deep Reinforcement Learning. ICML. arXiv:1602.01783
def worker(\theta, \varphi):
Initialize empty transition buffer \mathcal{D}.
Initialize the environment to the last state visited by this worker.
for n steps:
- Select an action using \pi_\theta, store the transition in the transition buffer.
for each transition in \mathcal{D}:
- Compute the n-step return in each state R^n_t = \displaystyle\sum_{k=0}^{n-1} \gamma^{k} \, r_{t+k+1} + \gamma^n \, V_\varphi(s_{t+n})
Compute policy gradient for the actor on the transition buffer: d\theta = \nabla_\theta \mathcal{J}(\theta) = \frac{1}{n} \sum_{t=1}^n \nabla_\theta \log \pi_\theta (s_t, a_t) \, (R^n_t - V_\varphi(s_t))
Compute value gradient for the critic on the transition buffer: d\varphi = \nabla_\varphi \mathcal{L}(\varphi) = -\frac{1}{n} \sum_{t=1}^n (R^n_t - V_\varphi(s_t)) \, \nabla_\varphi V_\varphi(s_t)
return d\theta, d\varphi
A2C: global networks with synchronization
Initialize global actor \theta and critic \varphi.
Initialize K workers with a copy of the environment.
for t \in [0, T_\text{total}]:
for K workers in parallel:
- d\theta_k, d\varphi_k = worker(\theta, \varphi)
join()
Merge all gradients:
d\theta = \frac{1}{K} \sum_{i=1}^K d\theta_k \; ; \; d\varphi = \frac{1}{K} \sum_{i=1}^K d\varphi_k
- Update the actor and critic using gradient ascent/descent:
\theta \leftarrow \theta + \eta \, d\theta \; ; \; \varphi \leftarrow \varphi - \eta \, d\varphi
A3C: Asynchronous advantage actor-critic
The previous slide depicts A2C, the synchronous version of A3C.
A2C synchronizes the workers (threads), i.e. it waits for the K workers to finish their job before merging the gradients and updating the global networks.
A3C is asynchronous:
the partial gradients are applied to the global networks as soon as they are available.
No need to wait for all workers to finish their job.
As the workers are not synchronized, this means that one worker could be copying the global networks \theta and \varphi while another worker is writing them.
This is called a Hogwild! update: no locks, no semaphores. Many workers can read/write the same data.
It turns out NN are robust enough for this kind of updates.
A3C: asynchronous updates
Initialize actor \theta and critic \varphi.
Initialize K workers with a copy of the environment.
for K workers in parallel:
for t \in [0, T_\text{total}]:
Copy the global networks \theta and \varphi.
Compute partial gradients:
d\theta_k, d\varphi_k = \text{worker}(\theta, \varphi)
- Update the global actor and critic using the partial gradients:
\theta \leftarrow \theta + \eta \, d\theta_k
\varphi \leftarrow \varphi - \eta \, d\varphi_k
A3C: Asynchronous advantage actor-critic

A3C does not use an experience replay memory as DQN.
Instead, it uses multiple parallel workers to distribute learning.
Each worker has a copy of the actor and critic networks, as well as an instance of the environment.
Weight updates are synchronized regularly though a master network using Hogwild!-style updates (every n=5 steps!).
Because the workers learn different parts of the state-action space, the weight updates are not very correlated.
- It works best on shared-memory systems (multi-core) as communication costs between GPUs are huge.
Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T. P., Harley, T., et al. (2016). Asynchronous Methods for Deep Reinforcement Learning. ICML. arXiv:1602.01783
A3C : results
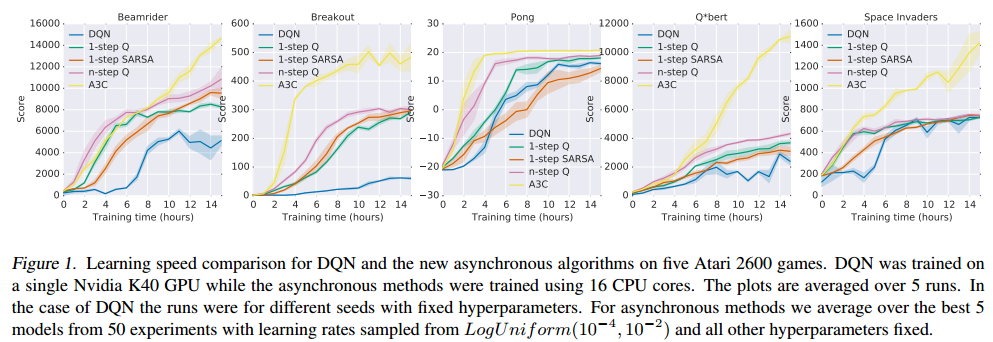
A3C set a new record for Atari games in 2016.
The main advantage is that the workers gather experience in parallel: training is much faster than with DQN.
LSTMs can be used to improve the performance.
Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T. P., Harley, T., et al. (2016). Asynchronous Methods for Deep Reinforcement Learning. ICML. arXiv:1602.01783
A3C : results
- Learning is only marginally better with more threads:
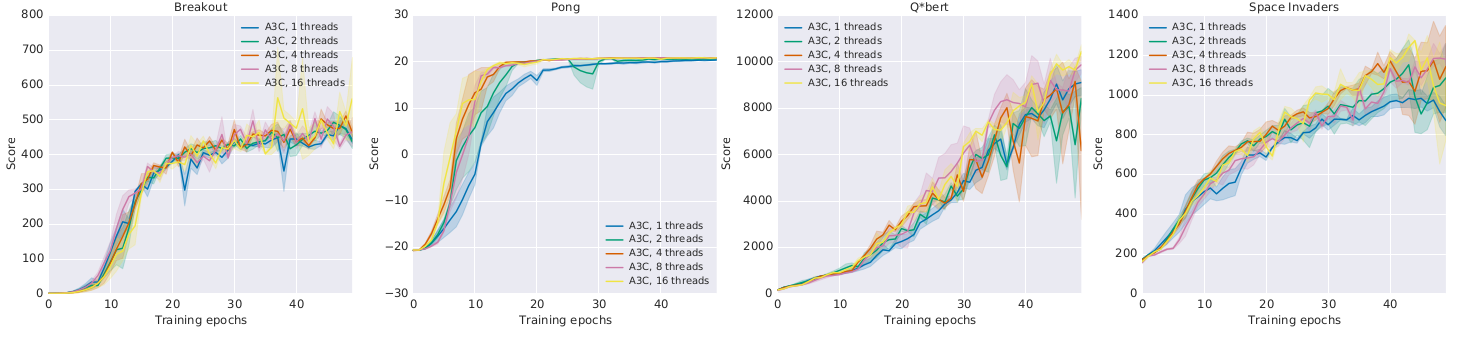
but much faster!
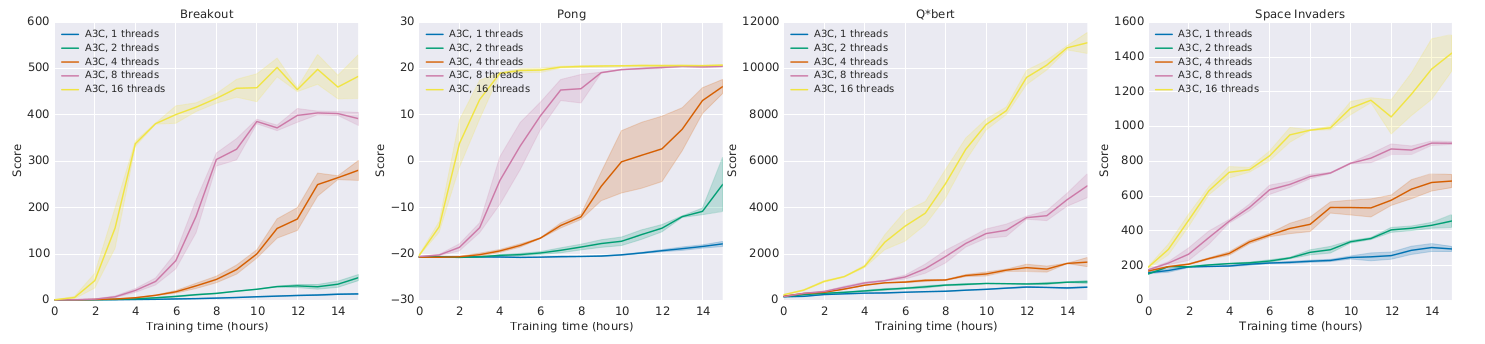
Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T. P., Harley, T., et al. (2016). Asynchronous Methods for Deep Reinforcement Learning. ICML. arXiv:1602.01783
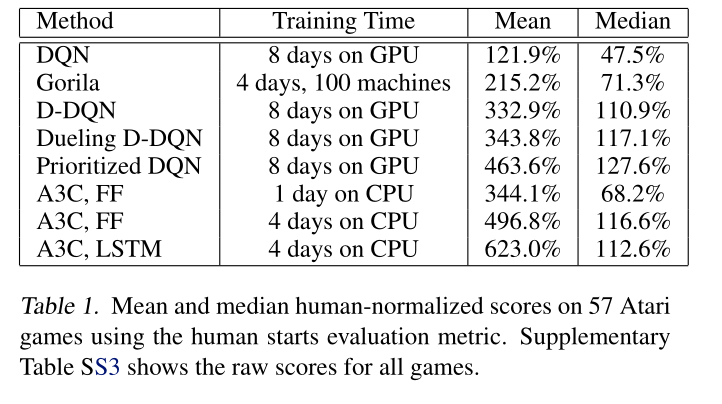
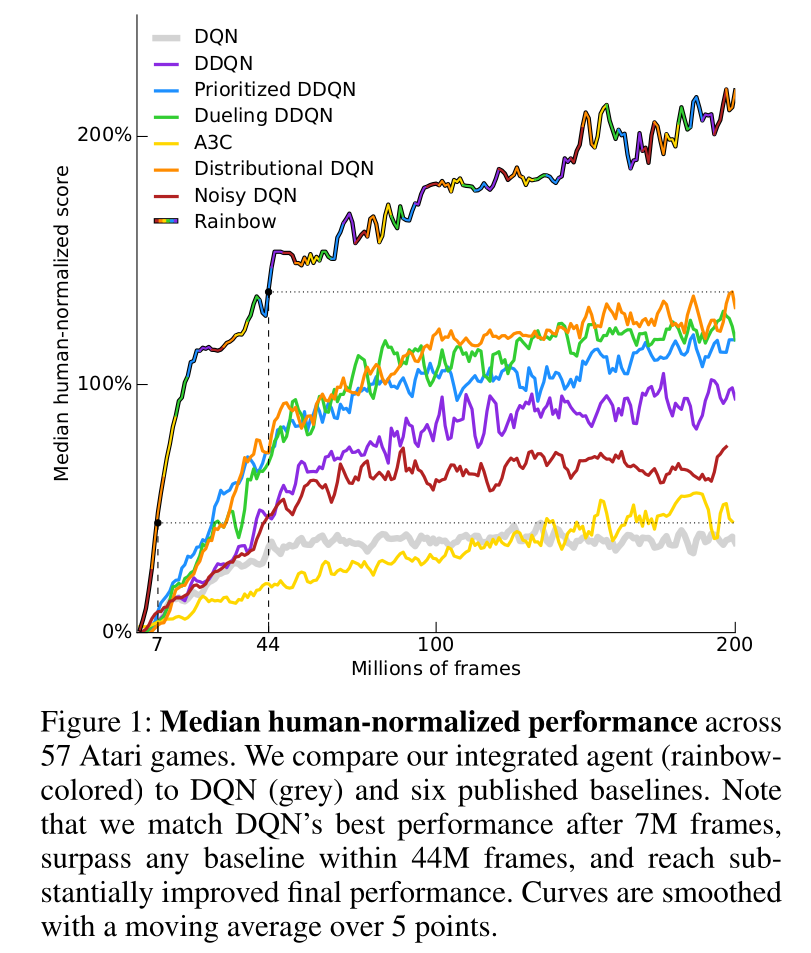
Comparison with DQN
- A3C came up in 2016. A lot of things happened since then…
2 - DDPG: Deep Deterministic Policy Gradient

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., et al. (2015). Continuous control with deep reinforcement learning. CoRR. arXiv:1509.02971.
Deterministic policy gradient theorem
- The objective function that we tried to maximize until now is :
\mathcal{J}(\theta) = \mathbb{E}_{\tau \sim \rho_\theta}[R(\tau)]
i.e. we want the returns of all trajectories generated by the stochastic policy \pi_\theta to be maximal.
It is equivalent to say that we want the value of all states visited by the policy \pi_\theta to be maximal:
- a policy \pi is better than another policy \pi' if its expected return is greater or equal than that of \pi' for all states s.
\pi > \pi' \Leftrightarrow V^{\pi}(s) > V^{\pi'}(s) \quad \forall s \in \mathcal{S}
- The objective function can be rewritten as:
\mathcal{J}'(\theta) = \mathbb{E}_{s \sim \rho_\theta}[V^{\pi_\theta}(s)]
where \rho_\theta is now the state visitation distribution, i.e. how often a state will be visited by the policy \pi_\theta.
Deterministic policy gradient theorem
- When introducing Q-values in each state, we obtain the following policy gradient:
g = \nabla_\theta \, \mathcal{J}(\theta) = \mathbb{E}_{s \sim \rho_\theta}[\nabla_\theta \, V^{\pi_\theta}(s)] = \mathbb{E}_{s \sim \rho_\theta}[\nabla_\theta \, \sum_a \pi_\theta(s, a) \, Q^{\pi_\theta}(s, a)]
This formulation necessitates to integrate overall possible actions:
Not possible with continuous action spaces.
The stochastic policy adds a lot of variance.
What would happen if the policy were deterministic, i.e. it always takes a single action in state s?
We can note this deterministic policy \mu_\theta(s), with:
\begin{aligned} \mu_\theta : \; \mathcal{S} & \rightarrow \mathcal{A} \\ s & \; \rightarrow \mu_\theta(s) \\ \end{aligned}
- The policy gradient becomes only stochastic regarding the visited states:
g = \nabla_\theta \, \mathcal{J}(\theta) = \mathbb{E}_{s \sim \rho_\theta}[\nabla_\theta \, Q^{\mu_\theta}(s, \mu_\theta(s))]
Deterministic policy gradient theorem
- The deterministic policy gradient is:
g = \nabla_\theta \, \mathcal{J}(\theta) = \mathbb{E}_{s \sim \rho_\theta}[\nabla_\theta \, Q^{\pi_\theta}(s, \mu_\theta(s))]
- We can now use the chain rule to decompose the gradient of Q^{\mu_\theta}(s, \mu_\theta(s)):
\nabla_\theta \, Q^{\mu_\theta}(s, \mu_\theta(s)) = \nabla_a \, Q^{\mu_\theta}(s, a)|_{a = \mu_\theta(s)} \times \nabla_\theta \, \mu_\theta(s)
\nabla_a \, Q^{\mu_\theta}(s, a)|_{a = \mu_\theta(s)} means that we differentiate Q^{\mu_\theta} w.r.t. a, and evaluate it in \mu_\theta(s).
- a is a variable, but \mu_\theta(s) is a deterministic value (constant).
\nabla_\theta \, \mu_\theta(s) tells how the output of the policy network varies with the parameters of NN:
- Automatic differentiation frameworks such as tensorflow can tell you that.
Deterministic policy gradient theorem
For any MDP, the deterministic policy gradient is:
\nabla_\theta \, \mathcal{J}(\theta) = \mathbb{E}_{s \sim \rho_\theta}[\nabla_a \, Q^{\mu_\theta}(s, a)|_{a = \mu_\theta(s)} \times \nabla_\theta \, \mu_\theta(s)]
The true Q-value Q^{\mu_\theta}(s, a) can even be safely replaced with an estimate Q_\varphi(s, a).
We come back to an actor-critic architecture:
The deterministic actor \mu_\theta(s) selects a single action in state s.
The critic Q_\varphi(s, a) estimates the value of that action.
Silver, D., Lever, G., Heess, N., Degris, T., Wierstra, D., and Riedmiller, M. (2014). Deterministic Policy Gradient Algorithms. ICML.
Deterministic Policy Gradient as an actor-critic architecture
Training the actor:
\nabla_\theta \mathcal{J}(\theta) = \mathbb{E}_{s \sim \rho_\theta}[\nabla_\theta \, \mu_\theta(s) \times \nabla_a Q_\varphi(s, a) |_{a = \mu_\theta(s)}]
Training the critic:
\mathcal{L}(\varphi) = \mathbb{E}_{s \sim \rho_\theta}[(r(s, \mu_\theta(s)) + \gamma \, Q_\varphi(s', \mu_\theta(s')) - Q_\varphi(s, \mu_\theta(s)))^2]
DDPG is off-policy
- If you act off-policy, i.e. you visit the states s using a behavior policy b, you would theoretically need to correct the policy gradient with importance sampling:
\nabla_\theta \mathcal{J}(\theta) = \mathbb{E}_{s \sim \rho_b}[\sum_a \, \frac{\pi_\theta(s, a)}{b(s, a)} \, \nabla_\theta \, \mu_\theta(s) \times \nabla_a Q_\varphi(s, a) |_{a = \mu_\theta(s)}]
But your policy is now deterministic: the actor only takes the action a=\mu_\theta(s) with probability 1, not \pi(s, a).
The importance weight is 1 for that action, 0 for the other. You can safely sample states from a behavior policy, it won’t affect the deterministic policy gradient:
\nabla_\theta \mathcal{J}(\theta) = \mathbb{E}_{s \sim \rho_b}[\nabla_\theta \, \mu_\theta(s) \times \nabla_a Q_\varphi(s, a) |_{a = \mu_\theta(s)}]
The critic uses Q-learning, so it is also off-policy.
DDPG is an off-policy actor-critic architecture!
DDPG: Deep Deterministic Policy Gradient
As DDPG is off-policy, an experience replay memory can be used to sample experiences.
The actor \mu_\theta learns using sampled transitions with DPG.
The critic Q_\varphi uses Q-learning on sampled transitions: target networks can be used to cope with the non-stationarity of the Bellman targets.
- Contrary to DQN, the target networks are not updated every once in a while, but slowly integrate the trained networks after each update (moving average of the weights):
\theta' \leftarrow \tau \theta + (1-\tau) \, \theta'
\varphi' \leftarrow \tau \varphi + (1-\tau) \, \varphi'
DDPG: Deep Deterministic Policy Gradient
A deterministic actor is good for learning (less variance), but not for exploring.
We cannot use \epsilon-greedy or softmax, as the actor outputs directly the policy, not Q-values.
For continuous actions, an exploratory noise can be added to the deterministic action:
a_t = \mu_\theta(s_t) + \xi_t
Ex: if the actor wants to move the joint of a robot by 2^o, it will actually be moved from 2.1^o or 1.9^o.
Ornstein-Uhlenbeck stochastic processes or parameter noise can be used for exploration.
Lilicrap et al. (2016). Continuous control with deep reinforcement learning. arXiv:1509.02971
Initialize actor network \mu_{\theta} and critic Q_\varphi, target networks \mu_{\theta'} and Q_{\varphi'}, ERM \mathcal{D} of maximal size N, random process \xi.
for t \in [0, T_\text{max}]:
Select the action a_t = \mu_\theta(s_t) + \xi and store (s_t, a_t, r_{t+1}, s_{t+1}) in the ERM.
For each transition (s_k, a_k, r_k, s'_k) in a minibatch of K transitions randomly sampled from \mathcal{D}:
- Compute the target value using target networks t_k = r_k + \gamma \, Q_{\varphi'}(s'_k, \mu_{\theta'}(s'_k)).
Update the critic by minimizing: \mathcal{L}(\varphi) = \frac{1}{K} \sum_k (t_k - Q_\varphi(s_k, a_k))^2
Update the actor by applying the deterministic policy gradient: \nabla_\theta \mathcal{J}(\theta) = \frac{1}{K} \sum_k \nabla_\theta \mu_\theta(s_k) \times \nabla_a Q_\varphi(s_k, a) |_{a = \mu_\theta(s_k)}
Update the target networks: \theta' \leftarrow \tau \theta + (1-\tau) \, \theta' \; ; \; \varphi' \leftarrow \tau \varphi + (1-\tau) \, \varphi'
DDPG: continuous control
DDPG: learning to drive in a day
DDPG: learning to drive in a day
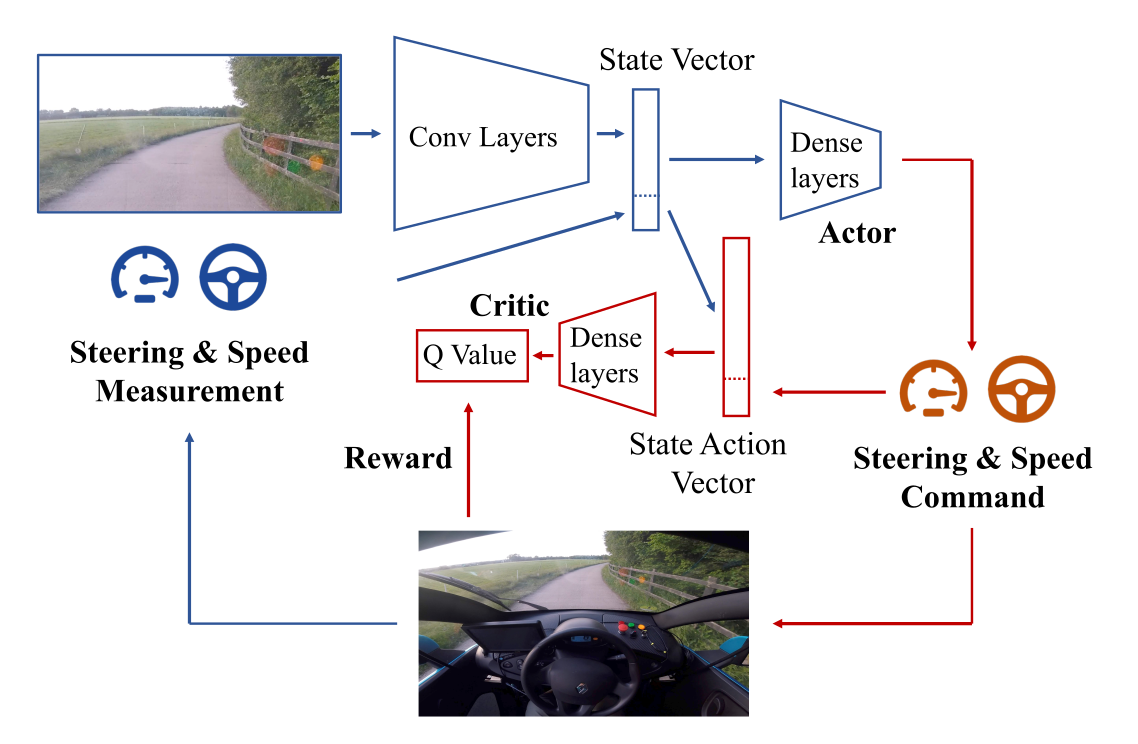
The algorithm is DDPG with prioritized experience replay. The Convnet is pretrained using an autoencoder.
Training is live, with an on-board NVIDIA Drive PX2 GPU.
A simulated environment is first used to find the hyperparameters.
Kendall, A., Hawke, J., Janz, D., Mazur, P., Reda, D., Allen, J.-M., et al. (2018). Learning to Drive in a Day. arXiv:1807.00412
3 - PPO: Proximal Policy Optimization

Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and Klimov, O. (2017). Proximal Policy Optimization Algorithms. arXiv:1707.06347.
Trust regions and gradients

Source: https://medium.com/@jonathan_hui/rl-trust-region-policy-optimization-trpo-explained-a6ee04eeeee9
The policy gradient tells you in which direction of the parameter space \theta the return is increasing the most.
If you take too big a step in that direction, the new policy might become completely bad (policy collapse).
Once the policy has collapsed, the new samples will all have a small return: the previous progress is lost.
This is especially true when the parameter space has a high curvature, which is the case with deep NN.
Policy collapse
Policy collapse is a huge problem in deep RL: the network starts learning correctly but suddenly collapses to a random agent.
For on-policy methods, all progress is lost: the network has to relearn from scratch, as the new samples will be generated by a bad policy.
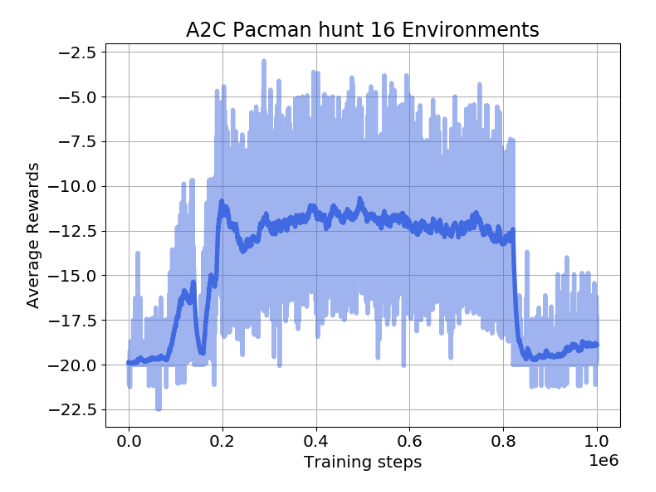
Oliver Lange (2019). Investigation of Model-Based Augmentation of Model-Free Reinforcement Learning Algorithms. MSc thesis, TU Chemnitz.
Trust regions and gradients
Reducing the learning rate only leads to slower learning (sample complexity), not safer convergence.
Trust region optimization searches in the neighborhood of the current parameters \theta which new value would maximize the return the most.
This is a constrained optimization problem: we still want to maximize the return of the policy, but by keeping the policy as close as possible from its previous value.

Source: https://medium.com/@jonathan_hui/rl-trust-region-policy-optimization-trpo-explained-a6ee04eeeee9
Trust regions and gradients
The size of the neighborhood determines the safety of the parameter change.
In safe regions, we can take big steps. In dangerous regions, we have to take small steps.
Problem: how can we estimate the safety of a parameter change?

Source: https://medium.com/@jonathan_hui/rl-trust-region-policy-optimization-trpo-explained-a6ee04eeeee9
TRPO: Trust Region Policy Optimization
- We want to maximize the expected return of a policy \pi_\theta, which is equivalent to maximizing the Q-value of every state-action pair visited by the policy:
\max_\theta \, \mathcal{J}(\theta) = \mathbb{E}_{s \sim \rho_\theta, a \sim \pi_\theta} [Q^{\pi_\theta}(s, a)]
Let’s note \theta_\text{old} the current value of the parameters of the policy \pi_{\theta_\text{old}}.
We search for a new policy \pi_\theta with parameters \theta which is always better than the current policy, i.e. where the Q-value of all actions is higher than with the current policy:
\max_\theta \, \mathcal{L}(\theta) = \mathbb{E}_{s \sim \rho_\theta, a \sim \pi_\theta} [Q_\theta(s, a) - Q_{\theta_\text{old}}(s, a)]
- The quantity
A^{\pi_{\theta_\text{old}}}(s, a) = Q_\theta(s, a) - Q_{\theta_\text{old}}(s, a)
is the advantage of taking the action (s, a) and thereafter following \pi_\theta, compared to following the current policy \pi_{\theta_\text{old}}.
Kakade, S., and Langford, J. (2002). Approximately Optimal Approximate Reinforcement Learning. Proc. 19th International Conference on Machine Learning, 267–274.
TRPO: Trust Region Policy Optimization
- If we can estimate the advantages and maximize them, we can find a new policy \pi_\theta with a higher return than the current one.
\mathcal{L}(\theta) = \mathbb{E}_{s \sim \rho_\theta, a \sim \pi_\theta} [A^{\pi_{\theta_\text{old}}}(s, a)] = \mathbb{E}_{s \sim \rho_\theta, a \sim \pi_\theta} [Q_\theta(s, a) - Q_{\theta_\text{old}}(s, a)]
- By definition, \mathcal{L}(\theta_\text{old}) = 0, so the policy maximizing \mathcal{L}(\theta) has positive advantages and is better than \pi_{\theta_\text{old}}.
\theta_\text{new} = \text{argmax}_\theta \; \mathcal{L}(\theta) \; \Rightarrow \; \mathcal{J}(\theta_\text{new}) \geq \mathcal{J}(\theta_\text{old})
- Maximizing the advantages ensures monotonic improvement: the new policy is always better than the previous one. Policy collapse is not possible!
Importance sampling
The problem is that we have to take samples (s, a) from the unknown policy \pi_\theta: we do not know it yet, as it is what we search. The only policy at our disposal to estimate the advantages is the current policy \pi_{\theta_\text{old}}.
We can use importance sampling with the current policy:
\mathcal{L}(\theta) = \mathbb{E}_{s \sim \rho_{\theta_\text{old}}, a \sim \pi_{\theta_\text{old}}} [\rho(s, a) \, A^{\pi_{\theta_\text{old}}}(s, a)]
with \rho(s, a) = \dfrac{\pi_{\theta}(s, a)}{\pi_{\theta_\text{old}}(s, a)} being the importance sampling weight.
The importance sampling weight \rho(s, a) introduces a lot of variance, worsening the sample complexity, and does not ensure that the update is safe.
Is there a way to make sure that \pi_\theta is not very different from \pi_{\theta_\text{old}}, therefore reducing the variance of the importance sampling weight?
TRPO (Trust Region Policy Optimization) uses Lagrange optimization with conjugate gradients to do that: complex.
PPO: Proximal Policy Optimization
- The solution introduced by PPO is simply to clip the importance sampling weight when it is too different from 1:
\mathcal{L}(\theta) = \mathbb{E}_{s \sim \rho_{\theta_\text{old}}, a \sim \pi_{\theta_\text{old}}} [\min(\rho(s, a) \, A^{\pi_{\theta_\text{old}}}(s, a), \text{clip}(\rho(s, a), 1-\epsilon, 1+\epsilon) \, A^{\pi_{\theta_\text{old}}}(s, a))]
For each sampled action (s, a), we use the minimum between:
the unconstrained objective with IS \rho(s, a) \, A^{\pi_{\theta_\text{old}}}(s, a).
the same, but with the IS weight clipped between 1-\epsilon and 1+\epsilon.
PPO: Proximal Policy Optimization
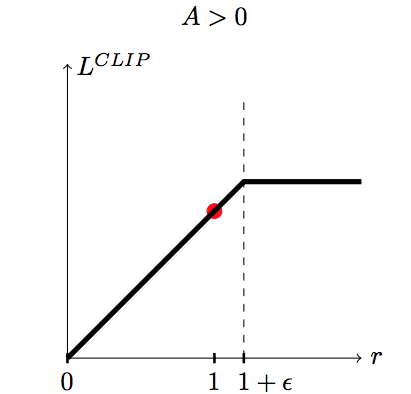
If the advantage A^{\pi_{\theta_\text{old}}}(s, a) is positive (better action than usual) and:
the IS is higher than 1+\epsilon, we use
(1+\epsilon) \, A^{\pi_{\theta_\text{old}}}(s, a).otherwise, we use \rho(s, a) \, A^{\pi_{\theta_\text{old}}}(s, a).
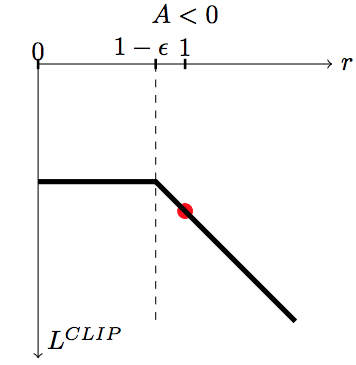
If the advantage A^{\pi_{\theta_\text{old}}}(s, a) is negative (worse action than usual) and:
the IS is lower than 1-\epsilon, we use
(1-\epsilon) \, A^{\pi_{\theta_\text{old}}}(s, a).otherwise, we use \rho(s, a) \, A^{\pi_{\theta_\text{old}}}(s, a).
This avoids changing too much the policy between two updates:
Good actions (A^{\pi_{\theta_\text{old}}}(s, a) > 0) do not become much more likely than before.
Bad actions (A^{\pi_{\theta_\text{old}}}(s, a) < 0) do not become much less likely than before.
Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and Klimov, O. (2017). Proximal Policy Optimization Algorithms. arXiv:1707.06347.
PPO: Proximal Policy Optimization
- The PPO clipped objective ensures than the importance sampling weight stays around one, so the new policy is not very different from the old one. It can learn from single transitions.
\mathcal{L}(\theta) = \mathbb{E}_{s \sim \rho_{\theta_\text{old}}, a \sim \pi_{\theta_\text{old}}} [\min(\rho(s, a) \, A^{\pi_{\theta_\text{old}}}(s, a), \text{clip}(\rho(s, a), 1-\epsilon, 1+\epsilon) \, A^{\pi_{\theta_\text{old}}}(s, a))]
It also has the monotonic improvement guarantee if \epsilon is chosen correctly.
The advantage of an action can be learned using any advantage estimator, for example the n-step advantage:
A^{\pi_{\theta_\text{old}}}(s_t, a_t) = \sum_{k=0}^{n-1} \gamma^{k} \, r_{t+k+1} + \gamma^n \, V_\varphi(s_{t+n}) - V_\varphi(s_{t})
Most implementations use Generalized Advantage Estimation (GAE, Schulman et al., 2015).
PPO is therefore an actor-critic method (as TRPO).
PPO is on-policy: it collects samples using distributed learning (as A3C) and then applies several updates to the actor and critic.
Schulman, J., Moritz, P., Levine, S., Jordan, M., and Abbeel, P. (2015). High-Dimensional Continuous Control Using Generalized Advantage Estimation. arXiv:1506.02438.
PPO : Mujoco control
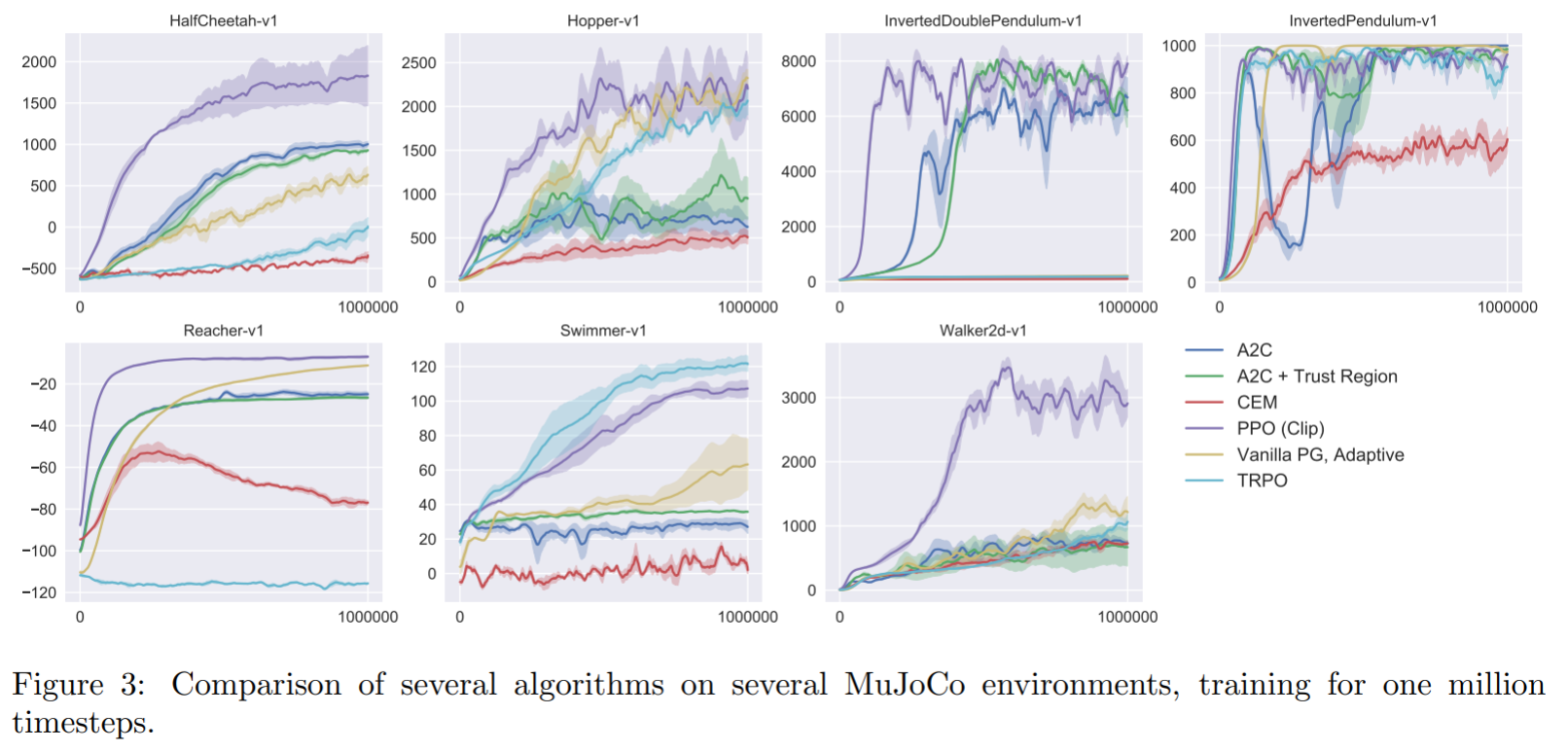
Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and Klimov, O. (2017). Proximal Policy Optimization Algorithms. arXiv:1707.06347.
PPO : Parkour
Check more robotic videos at: https://openai.com/blog/openai-baselines-ppo/
PPO: dexterity learning
PPO: ChatGPT
Source: https://openai.com/blog/chatgpt
twitter:ai-memes
OpenAI Five: Dota 2
Why is Dota 2 hard?

| Feature | Chess | Go | Dota 2 |
|---|---|---|---|
| Total number of moves | 40 | 150 | 20000 |
| Number of possible actions | 35 | 250 | 1000 |
| Number of inputs | 70 | 400 | 20000 |
OpenAI Five: Dota 2
- OpenAI Five is composed of 5 PPO networks (one per player), using 128,000 CPUs and 256 V100 GPUs.
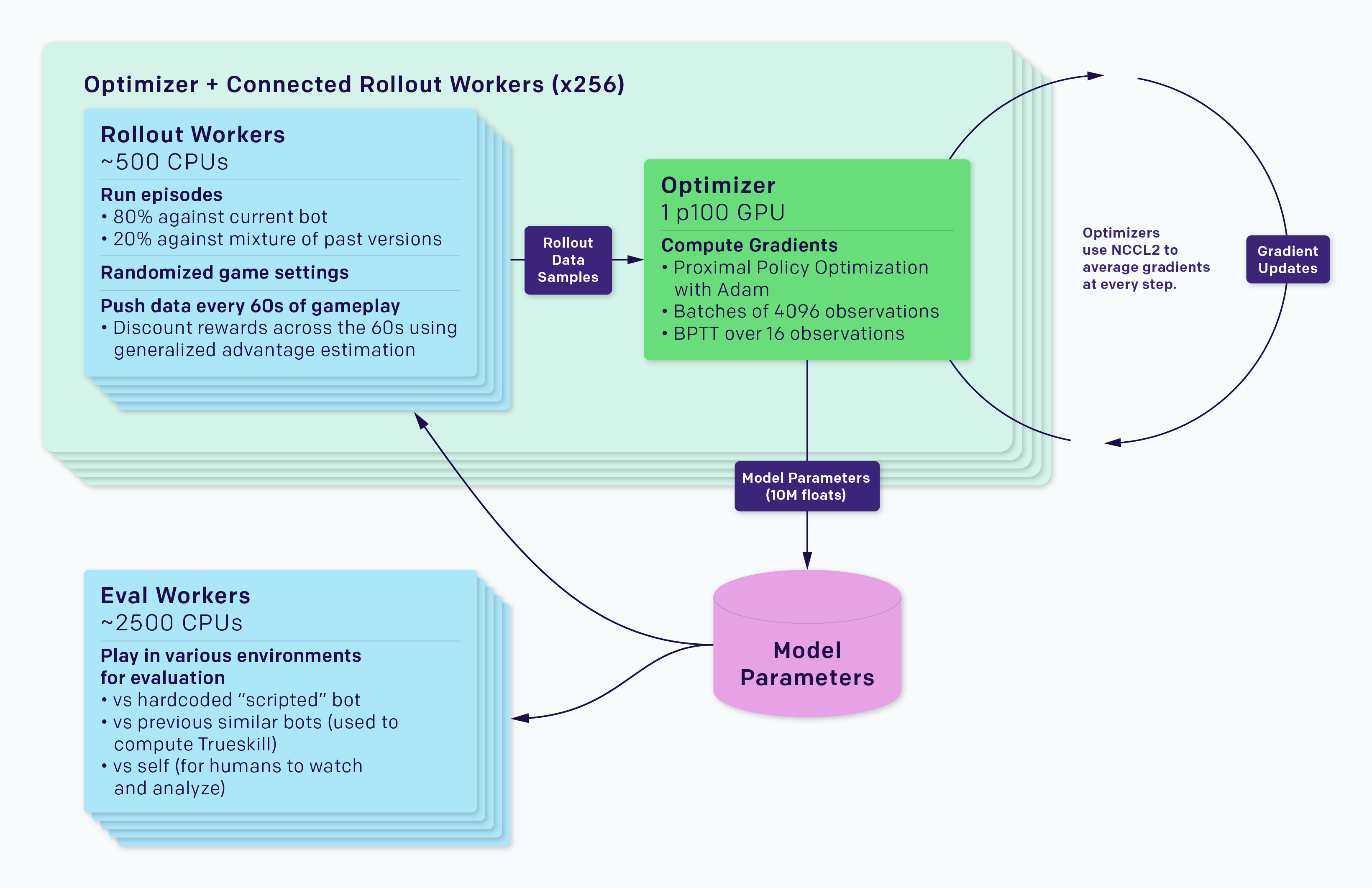
OpenAI Five: Dota 2
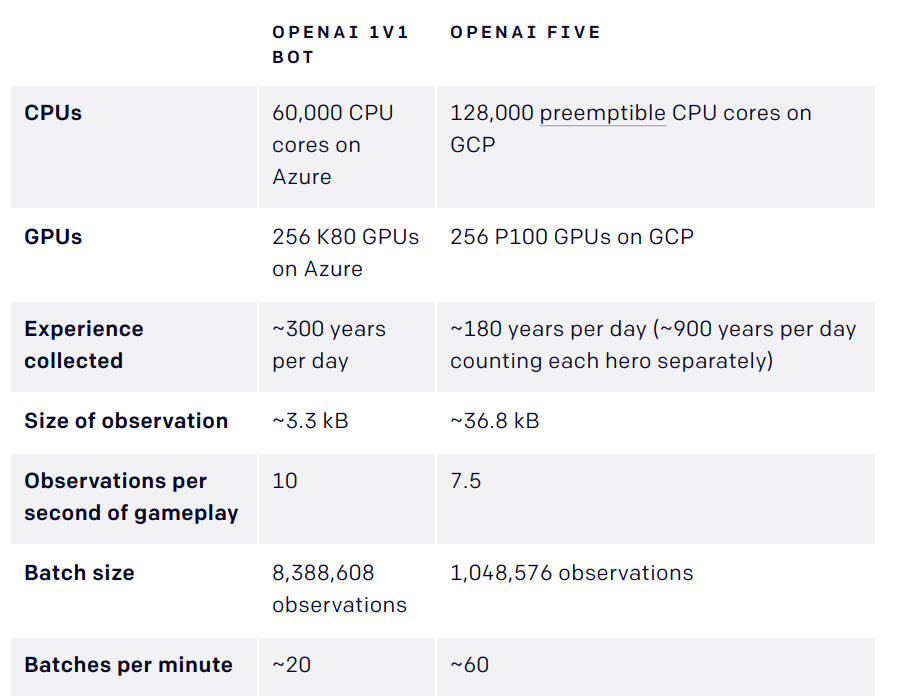
OpenAI Five: Dota 2
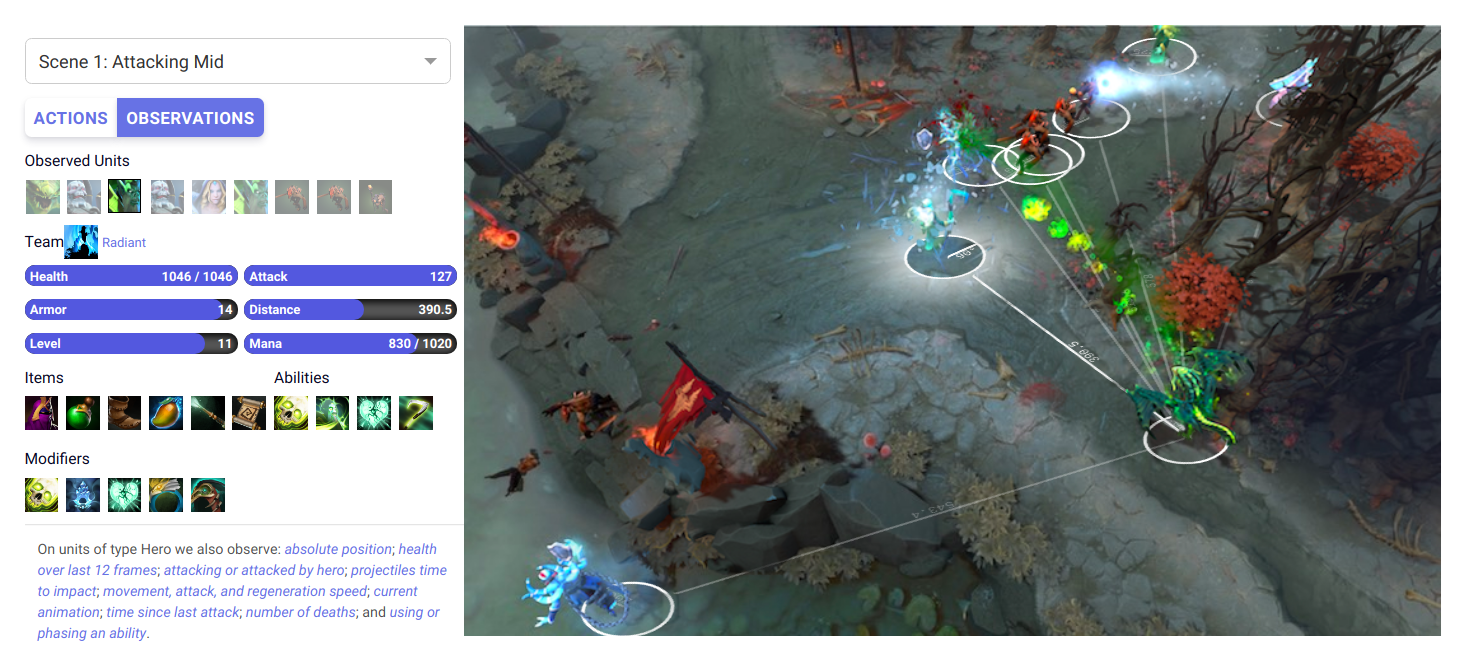
OpenAI Five: Dota 2
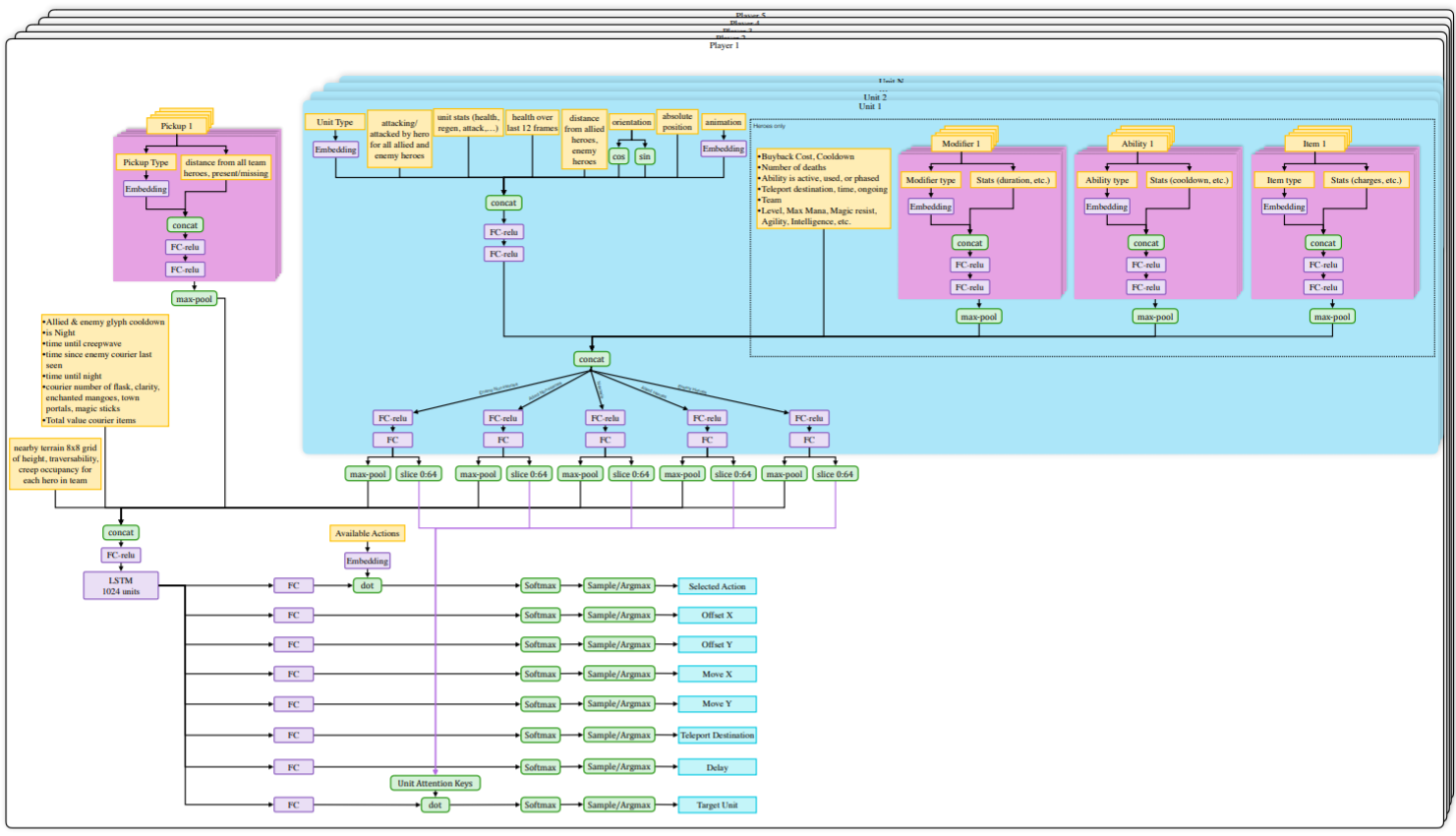
https://d4mucfpksywv.cloudfront.net/research-covers/openai-five/network-architecture.pdf
OpenAI Five: Dota 2
The agents are trained by self-play. Each worker plays against:
the current version of the network 80% of the time.
an older version of the network 20% of the time.
Reward is hand-designed using human heuristics:
- net worth, kills, deaths, assists, last hits…
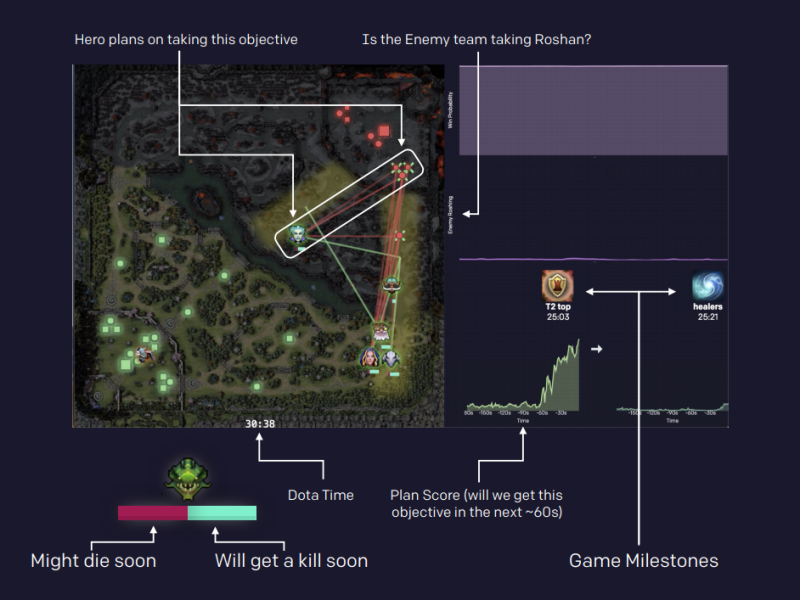
The discount factor \gamma is annealed from 0.998 (valuing future rewards with a half-life of 46 seconds) to 0.9997 (valuing future rewards with a half-life of five minutes).
Coordinating all the resources (CPU, GPU) is actually the main difficulty:
- Kubernetes, Azure, and GCP backends for Rapid, TensorBoard, Sentry and Grafana for monitoring…